Parallel filtering and smoothing in an LG-SSM#
This notebook shows how can reduce the cost of inference from linear to logarithmic in time, if we have a GPU device. Rather than running a Kalman filter/smoother sequentially in time, you can use a parallel (associative) scan to compute the filtering and smoothing distributions using a parallel algorithm that requires \(O(T)\) parallel processors, but can run in only \(O(\log T)\) time. This is the key innovation behind modern “deep” state space models like S5 (Smith et al., 2023) and Mamba (Gu and Dao, 2024). The core algorithm is nicely described by Särkkä and Garćıa-Ferńandez (2020).
This notebook is adapted from an example notebook by Adrien Correnflos. Some small changes have been made so it works with dynamax.
If you have a GPU, you should be able to get a speedup curve like this:
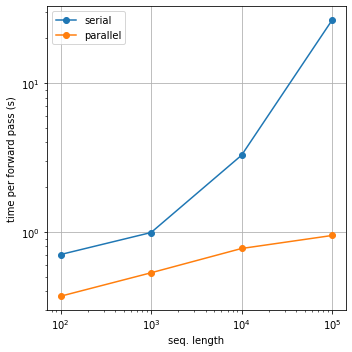
Similar algorithms exist for HMMs (Hassan et al., 2021), which we have implemented in dynamax.hidden_markov_model.parallel_inference
References#
Särkkä, Simo, and Ángel F. García-Fernández. “Temporal parallelization of Bayesian smoothers.” IEEE Transactions on Automatic Control 66.1 (2020): 299-306.
Smith, Jimmy TH, Andrew Warrington, and Scott Linderman. “Simplified State Space Layers for Sequence Modeling.” The Eleventh International Conference on Learning Representations.
Gu, Albert, and Tri Dao. “Mamba: Linear-time sequence modeling with selective state spaces.” arXiv preprint arXiv:2312.00752 (2023).
Hassan, Syeda Sakira, Simo Särkkä, and Ángel F. García-Fernández. “Temporal parallelization of inference in hidden Markov models.” IEEE Transactions on Signal Processing 69 (2021): 4875-4887.
Setup#
Show code cell content
%%capture
try:
import dynamax
except ModuleNotFoundError:
print('installing dynamax')
%pip install -q dynamax[notebooks]
import dynamax
import jax
from jax import numpy as jnp
from jax import random as jr
from jax import block_until_ready
from matplotlib import pyplot as plt
import time
from dynamax.linear_gaussian_ssm import lgssm_smoother, parallel_lgssm_smoother
from dynamax.linear_gaussian_ssm import LinearGaussianSSM
print(jax.devices())
print(jax.devices()[0].platform)
if jax.devices()[0].platform == 'cpu':
cpu_mode = True
else:
cpu_mode = False
[CpuDevice(id=0)]
cpu
Model#
The model is a simple tracking model (see Example 3.6 in Bayesian Filtering and Smoothing (S. Särkkä, 2013).
dt = 0.1
F = jnp.eye(4) + dt * jnp.eye(4, k=2)
Q = 1. * jnp.kron(jnp.array([[dt**3/3, dt**2/2],
[dt**2/2, dt]]),
jnp.eye(2))
H = jnp.eye(2, 4)
R = 0.5 ** 2 * jnp.eye(2)
μ0 = jnp.array([0.,0.,1.,-1.])
Σ0 = jnp.eye(4)
latent_dim = 4
observation_dim = 2
input_dim = 0
lgssm = LinearGaussianSSM(latent_dim, observation_dim)
params, _ = lgssm.initialize(
initial_mean=μ0,
initial_covariance= Σ0,
dynamics_weights=F,
dynamics_covariance=Q,
emission_weights=H,
emission_covariance=R)
Test parallel inference on a single sequence#
num_timesteps = 100
key = jr.PRNGKey(0)
key, subkey = jr.split(key)
z,emissions = lgssm.sample(params, subkey, num_timesteps)
ssm_posterior = lgssm_smoother(params, emissions)
parallel_posterior = parallel_lgssm_smoother(params, emissions)
print(parallel_posterior.filtered_means.shape)
print(parallel_posterior.filtered_covariances.shape)
(100, 4)
(100, 4, 4)
assert jnp.allclose(parallel_posterior.filtered_means, ssm_posterior.filtered_means, atol=1e-3)
assert jnp.allclose(parallel_posterior.filtered_covariances, ssm_posterior.filtered_covariances, atol=1e-3)
assert jnp.allclose(parallel_posterior.smoothed_means, ssm_posterior.smoothed_means, atol=1e-3)
assert jnp.allclose(parallel_posterior.smoothed_covariances, ssm_posterior.smoothed_covariances, atol=1e-3)
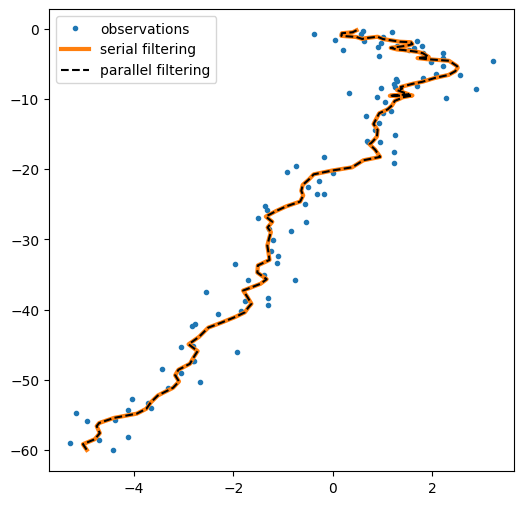
plt.figure(figsize=(6,6))
plt.plot(*emissions.T,'.', label="observations")
plt.plot(*ssm_posterior.filtered_means[:,:2].T, label="serial filtering", lw=3)
plt.plot(*parallel_posterior.filtered_means[:,:2].T, "--k", label="parallel filtering");
plt.legend();
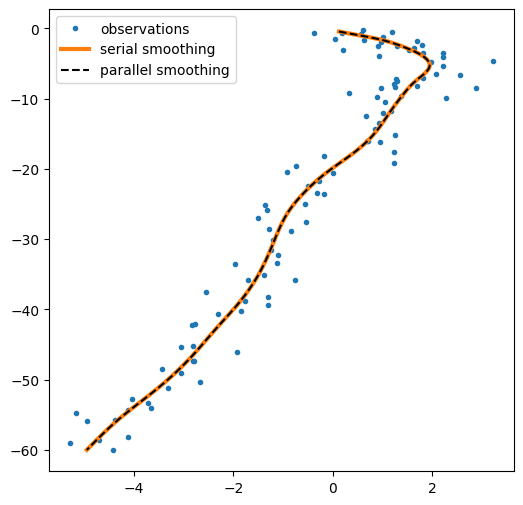
plt.figure(figsize=(6,6))
plt.plot(*emissions.T,'.', label="observations")
plt.plot(*ssm_posterior.smoothed_means[:,:2].T, lw=3,label="serial smoothing")
plt.plot(*parallel_posterior.smoothed_means[:,:2].T, "--k", label="parallel smoothing")
plt.legend();
Timing comparison#
key = jr.PRNGKey(0)
if cpu_mode:
Ts = [100, 200, 500]
num_repeats = 1
else:
Ts = [100, 1_000, 10_000, 100_000]
num_repeats = 3
serial_smoothing_durations = []
parallel_smoothing_durations = []
compiled = False
for T in Ts:
key, subkey = jr.split(key)
z,emissions = lgssm.sample(params, subkey, T)
if not compiled:
ssm_posterior = block_until_ready(lgssm_smoother(params, emissions))
parallel_posterior = block_until_ready(parallel_lgssm_smoother(params, emissions))
start = time.time()
for _ in range(num_repeats):
ssm_posterior = block_until_ready(lgssm_smoother(params, emissions))
end = time.time()
mean_time = (end-start)/num_repeats
serial_smoothing_durations.append(mean_time)
print(f"Num timesteps={T}, \t time serial = {mean_time}")
start = time.time()
for _ in range(num_repeats):
parallel_posterior = block_until_ready(parallel_lgssm_smoother(params, emissions))
end = time.time()
mean_time = (end-start)/num_repeats
parallel_smoothing_durations.append(mean_time)
print(f"Num timesteps={T}, \t time parallel = {mean_time}")
Num timesteps=100, time serial = 0.2555084228515625
Num timesteps=100, time parallel = 0.23434233665466309
Num timesteps=200, time serial = 0.26387524604797363
Num timesteps=200, time parallel = 0.26383018493652344
Num timesteps=500, time serial = 0.2693517208099365
Num timesteps=500, time parallel = 0.297931432723999
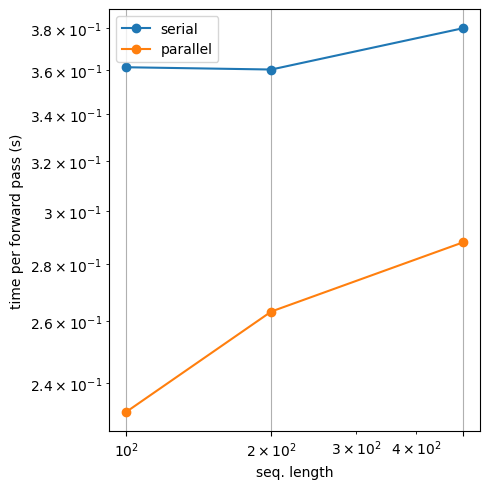
plt.figure(figsize=(5, 5))
plt.loglog(Ts, serial_smoothing_durations, '-o', label='serial')
plt.loglog(Ts, parallel_smoothing_durations, '-o', label='parallel')
plt.xticks(Ts)
plt.xlabel("seq. length")
plt.ylabel("time per forward pass (s)")
plt.grid(True)
plt.legend()
plt.tight_layout()
