Online learning of an MLP Classifier using conditional moments Gaussian filter#
This notebook is similar to the previous notebook that demonstrated how to use CMGF for online Bayesian logistic regression. Here, we perform sequential (recursive) Bayesian inference for the parameters of a binary MLP classifier. To do this, we treat the parameters of the model as the unknown hidden states. We assume that these are approximately constant over time (we add a small amount of Gaussian drift, for numerical stability.) The graphical model is shown below.
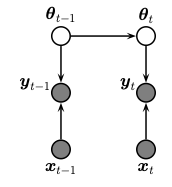
The model has the following form
This is a generalized Gaussian SSM, where the observation model is non-linear and non-Gaussian.
To perform approximate inference, using the conditional moments Gaussian filter (CMGF). We approximate the relevant integrals using the extended Kalman filter. For more details, see sec 8.7.7 of Probabilistic Machine Learning: Advanced Topics.
Video of training: https://gist.github.com/petergchang/9441b853b889e0b47d0622da8f7fe2f6
Setup#
%%capture
try:
import dynamax
except ModuleNotFoundError:
print('installing dynamax')
%pip install -q dynamax[notebooks]
import dynamax
from dynamax.generalized_gaussian_ssm import ParamsGGSSM, EKFIntegrals
from dynamax.generalized_gaussian_ssm import conditional_moments_gaussian_filter
try:
import flax.linen as nn
except ModuleNotFoundError:
print('installing flax')
%pip install -qq flax
import flax.linen as nn
from typing import Sequence
from functools import partial
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import jax
import jax.numpy as jnp
import jax.random as jr
from jax.flatten_util import ravel_pytree
Helper function to plot the posterior predictive distribution#
# Helper function that visualizes 2d posterior predictive distribution
def plot_posterior_predictive(ax, X, Y, title, Xspace=None, Zspace=None, cmap=cm.rainbow):
if Xspace is not None and Zspace is not None:
ax.contourf(*(Xspace.T), (Zspace.T[0]), cmap=cmap, levels=50)
ax.axis('off')
colors = ['red' if y else 'blue' for y in Y]
ax.scatter(*X.T, c=colors, edgecolors='black', s=50)
ax.set_title(title)
return ax
Create data#
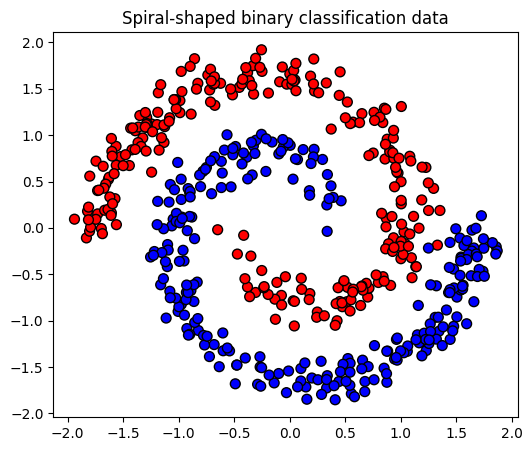
First, we generate a binary spiral data.
# Generate spiral dataset
# Adapted from https://gist.github.com/45deg/e731d9e7f478de134def5668324c44c5
def generate_spiral_dataset(key=0, num_per_class=250, zero_var=1., one_var=1., shuffle=True):
if isinstance(key, int):
key = jr.PRNGKey(key)
key1, key2, key3, key4 = jr.split(key, 4)
theta = jnp.sqrt(jr.uniform(key1, shape=(num_per_class,))) * 2*jnp.pi
r = 2*theta + jnp.pi
generate_data = lambda theta, r: jnp.array([jnp.cos(theta)*r, jnp.sin(theta)*r]).T
# Data for output zero
zero_input = generate_data(theta, r) + zero_var * jr.normal(key2, shape=(num_per_class, 2))
zero_output = jnp.zeros((num_per_class, 1,))
# Data for output one
one_input = generate_data(theta, -r) + one_var * jr.normal(key3, shape=(num_per_class, 2))
one_output = jnp.ones((num_per_class, 1,))
# Stack the inputs and standardize
input = jnp.concatenate([zero_input, one_input])
input = (input - input.mean(axis=0)) / input.std(axis=0)
# Generate binary output
output = jnp.concatenate([jnp.zeros(num_per_class), jnp.ones(num_per_class)])
if shuffle:
idx = jr.permutation(key4, num_per_class * 2)
input, output = input[idx], output[idx]
return input, output
# Generate data
input, output = generate_spiral_dataset()
# Plot data
fig, ax = plt.subplots(figsize=(6, 5))
title = "Spiral-shaped binary classification data"
plot_posterior_predictive(ax, input, output, title);
Plotting code#
Next, let us define a grid on which we compute the predictive distribution.
# Define grid limits
xmin, ymin = input.min(axis=0) - 0.1
xmax, ymax = input.max(axis=0) + 0.1
# Define grid
step = 0.1
x_grid, y_grid = jnp.meshgrid(jnp.mgrid[xmin:xmax:step], jnp.mgrid[ymin:ymax:step])
input_grid = jnp.concatenate([x_grid[...,None], y_grid[...,None]], axis=2)
Next, we define a function to that returns the posterior predictive probability for each point in grid.
# 'binary=True' indicates rounding probabilities to binary outputs
def posterior_predictive_grid(grid, mean, apply, binary=False):
inferred_fn = lambda x: apply(mean, x)
fn_vec = jnp.vectorize(inferred_fn, signature='(2)->(3)')
Z = fn_vec(grid)
if binary:
Z = jnp.rint(Z)
return Z
Define MLP#
Finally, we define a generic MLP class that uses a sigmoid activation function.
class MLP(nn.Module):
features: Sequence[int]
@nn.compact
def __call__(self, x):
for feat in self.features[:-1]:
x = nn.relu(nn.Dense(feat)(x))
x = nn.Dense(self.features[-1])(x)
return x
def get_mlp_flattened_params(model_dims, key=0):
if isinstance(key, int):
key = jr.PRNGKey(key)
# Define MLP model
input_dim, features = model_dims[0], model_dims[1:]
model = MLP(features)
dummy_input = jnp.ones((input_dim,))
# Initialize parameters using dummy input
params = model.init(key, dummy_input)
flat_params, unflatten_fn = ravel_pytree(params)
# Define apply function
def apply(flat_params, x, model, unflatten_fn):
return model.apply(unflatten_fn(flat_params), jnp.atleast_1d(x))
apply_fn = partial(apply, model=model, unflatten_fn=unflatten_fn)
return model, flat_params, unflatten_fn, apply_fn
Online Training Using CMGF-EKF#
# Define MLP architecture
input_dim, hidden_dims, output_dim = 2, [15, 15], 1
model_dims = [input_dim, *hidden_dims, output_dim]
_, flat_params, _, apply_fn = get_mlp_flattened_params(model_dims)
# Some model parameters and helper function
state_dim, emission_dim = flat_params.size, output_dim
sigmoid_fn = lambda w, x: jax.nn.sigmoid(apply_fn(w, x))
# Run CMGF-EKF to train the MLP Classifier
cmgf_ekf_params = ParamsGGSSM(
initial_mean=flat_params,
initial_covariance=jnp.eye(state_dim),
dynamics_function=lambda w, x: w,
dynamics_covariance=jnp.eye(state_dim) * 1e-4,
emission_mean_function = lambda w, x: sigmoid_fn(w, x),
emission_cov_function = lambda w, x: sigmoid_fn(w, x) * (1 - sigmoid_fn(w, x))
)
cmgf_ekf_post = conditional_moments_gaussian_filter(cmgf_ekf_params, EKFIntegrals(), output, inputs=input)
# Extract history of filtered weight values
w_means, w_covs = cmgf_ekf_post.filtered_means, cmgf_ekf_post.filtered_covariances
# Evaluate the trained MLP on input_grid
Z = posterior_predictive_grid(input_grid, w_means[-1], sigmoid_fn, binary=False)
# Plot the final result
fig, ax = plt.subplots(figsize=(6, 5))
title = "CMGF-EKF One-Pass Trained MLP Classifier"
plot_posterior_predictive(ax, input, output, title, input_grid, Z);
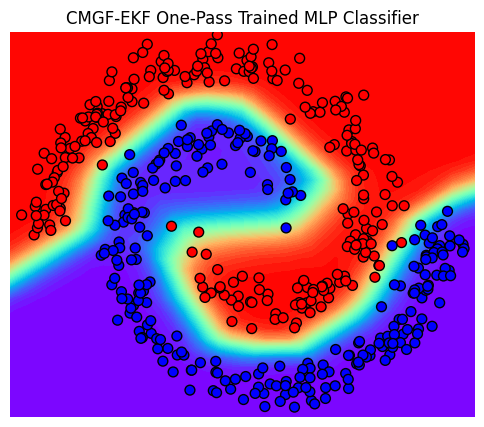
Next, we visualize the training procedure by evaluating the intermediate steps.
intermediate_steps = [9, 49, 99, 199, 299, 399]
fig, ax = plt.subplots(3, 2, figsize=(8, 10))
for step, axi in zip(intermediate_steps, ax.flatten()):
Zi = posterior_predictive_grid(input_grid, w_means[step], sigmoid_fn)
title = f'step={step+1}'
plot_posterior_predictive(axi, input[:step+1], output[:step+1], title, input_grid, Zi)
plt.tight_layout()
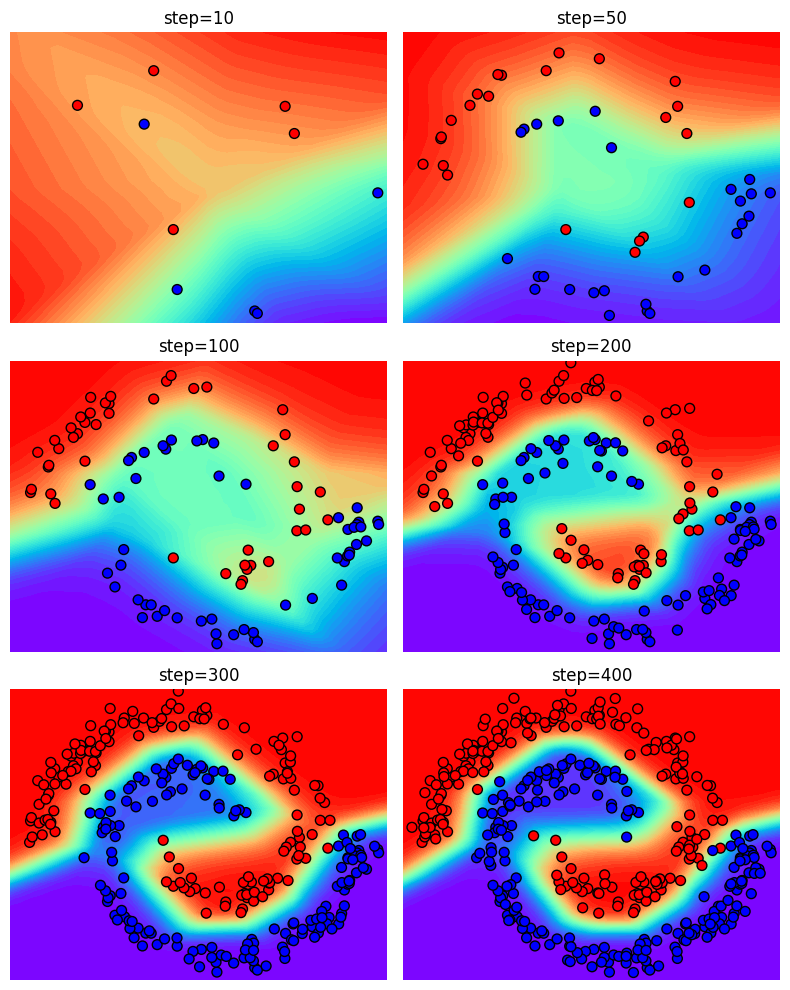
Animation#
Finally, we generate a video of the MLP-Classifier being trained.
Note: This code is commented out by default since it takes a while time to run.
# import matplotlib.animation as animation
# from IPython.display import HTML
# def animate(i):
# ax.cla()
# w_curr = w_means[i]
# Zi = posterior_predictive_grid(input_grid, w_means[i], sigmoid_fn)
# title = f'CMGF-EKF-MLP ({i+1}/500)'
# plot_posterior_predictive(ax, input[:i+1], output[:i+1], title, input_grid, Zi)
# return ax
# fig, ax = plt.subplots(figsize=(6, 5))
# anim = animation.FuncAnimation(fig, animate, frames=500, interval=50)
# anim.save("cmgf_mlp_classifier.mp4", dpi=200, bitrate=-1, fps=24)
# HTML(anim.to_html5_video())


